Problem Description
Given Some inequality on some variable (Xi , Xj , …. ) in form
Xj – Xi <= W
We need to determine whether we can assign values to variables so that all the given inequality is satisfiable or not ? If satisfiable, then output A solution.
This System is called System of difference constraints. This is a special case of linear programming and yet very much useful.
Solution
Believe it or not, This problem has an elegant solution using Shortest Path algorithm.
To understand Please go through this :
1. lec18
2. Introduction To Algorithm (3rd Edition) : 24.4 Section
So I am writing the results (no proof). Proofs are discussed in details in the suggested readings.
Constraint Graph
– For each variable we create a vertex.
– For each in-equality, Xj – Xi <= W , We give an edge (Vi,Vj) with cost W

– Create a source vertex (S) and give an edge (S,Vi) with cost = 0 ( Without using source vertex,we can solve)
Example:
Finding values for the unknowns x1,x2,x3,x4,x5, satisfying the following 8 difference constraints
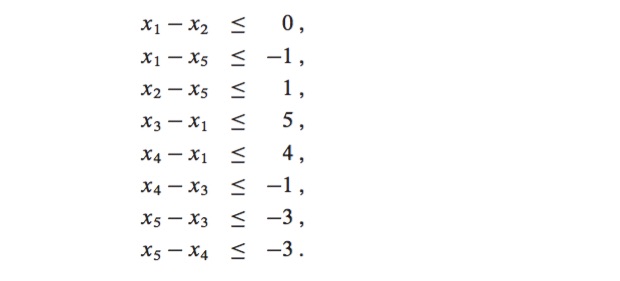
Constraint Graph with Solutions:

Unsatisfiable constraints
Theorem. If the constraint graph contains a negative-weight cycle, then the system of differences is unsatisfiable.
Proof is given in the pdf file.
Now we know if there is a solution or not.
Determining a Possible Solution :
– If there is no negative cycle in the constraint graph, Then There is a solution for the system. One of the solution is
for each variable (Xi):
Xi = Shortest Path distance of Vi from the Source vertex in Constraint Graph.
What about other solutions???
Let x = {x1,x2,…, xn } be a solution to a system of difference con- straints, and let d be any constant. Then x + d = { x1 + d, x2 + d, . . . , xn + d } is a solution as well.
Shortest Path can be calculated from Bellman-Ford algorithm.
Other Results from The constraint Graph:
# Bellman-Ford maximizes x1 + x2 + …. + xn subject to the constraints xj – xi ≤ wij and xi ≤ 0
# Bellman-Ford also minimizes maximum{xi} – minimum {xi}
Practise Problem:
1. Uva 11478
Solution:
For each node v in the given graph, Create a variable such that we have operated Halum (v,
) on the vertex v.
We then Binary Search on the answer.
Let Ans = X. We need to determine is X can possibly be our answer.
for each edge (u,v) , We get,
This is just difference constraint discussed above. We can check whether we can satisfy all these conditions.
Lastly output the maximal answer.
Click to See Code
#include <bits/stdc++.h>
using namespace std;
struct Edge{
int u,v,w;
};
vector<Edge>edge;
int n,e,u,v,w;
vector<pair<int,int > >G[505];
int d[505];
bool inq[505];
int Times[505];
bool spfa()
{
queue<int>q; // I have omitted Source vertex by pushing all the variables in queue with distance = 0
for(int i = 1;i <= n; i ++ ) {
d[i]= 0;
q.push(i);
inq[i] = 1;
Times[i] = 1;
}
while(!q.empty()){
int u = q.front(); q.pop();
inq[u] = 0;
for(int i = 0; i < G[u].size(); i ++ ) {
int v = G[u][i].first, w = G[u][i].second;
if(d[v] > d[u] + w) {
d[v] = d[u] + w;
if(inq[v] == 0) {
inq[v] = 1;
q.push(v);
Times[v] ++;
if(Times[v] > n+2 ) return 0;
}
}
}
}
return 1;
}
bool can(int Mid)
{
for(int i = 0; i <= n; i ++ ) {
G[i].clear();
}
for(int i = 0; i < e; i ++ ) {
u = edge[i].u, v = edge[i].v , w = edge[i].w ;
G[u].push_back(make_pair(v,w - Mid));
}
return spfa();
}
int main()
{
while(scanf("%d %d",&n,&e)==2) {
edge.clear();
for(int i = 0; i < e; i ++ ) {
scanf("%d %d %d",&u,&v,&w);
edge.push_back({u,v,w});
}
if(can(10001)) {
printf("Infinite\n");
continue;
}
int low = 1, high = 10000, mid, ans = -1;
while(low <= high ) {
mid = (low+high) /2;
if(can(mid)) {
ans = mid;
low = mid+1;
}
else high= mid-1;
}
if(ans == -1 ) printf("No Solution\n");
else printf("%d\n",ans);
edge.clear();
}
}
2. Uva 515 – King
3. POJ – 1201
4. POJ – 2983
5. POJ 1275
6. POJ – 3159
7. POJ – 3169